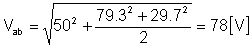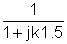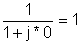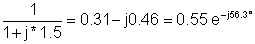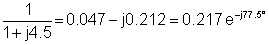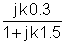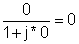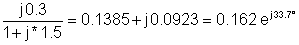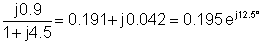Klicka eller Peka på exemplet kretsarna nedan för att aktivera TINACloud och välj det interaktiva DC-läget för att analysera dem online.
Få en låg kostnad tillgång till TINACloud för att redigera exemplen eller skapa egna kretsar

Smakämnen Fourier teorem säger att varje periodisk vågform kan syntetiseras genom att lägga till lämpligt vägda sinus- och kosinustermer av olika frekvenser. Satsen är väl täckt i andra läroböcker, så vi kommer bara att sammanfatta resultaten och visa några exempel.

Låt vår periodiska funktion vara f (t) = f (t ±nT) där T är tiden för en period och n är ett heltal.

w₀= 2p/ T den grundläggande vinkelfrekvensen.

Av Fourier teorem, den periodiska funktionen kan skrivas som följande summa:

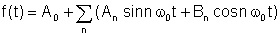
var

A_n och B_n är Fourier-koefficienterna och summan är Fourier-serier.

En annan form, förmodligen lite mer praktisk:

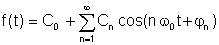
var

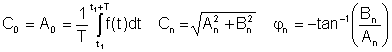
A₀ = C₀ är DC eller medelvärdet, A₁, B₁ och C₁ är de grundläggande komponenterna, och de andra är de harmoniska termerna.

Även om det bara krävs några få termer för att ungefärliga vågformer kommer andra att kräva många termer.

Generellt, ju fler termer som ingår, desto bättre är approximationen, men för vågformer som innehåller steg, såsom rektangulära impulser, Gibbs fenomen kommer in i spelet. När antalet termer ökar blir överskridningen koncentrerad i en allt mindre tid.

An jämn funktion f (t) = f (-t) (axelsymmetri) kräver endast kosinustermer.

An udda funktionen f (t) = - f (-t) (punktsymmetri) kräver endast sinustermer.

En vågform med spegel eller halvvågssymmetri har bara udda harmonier i sin Fourier-representation.

Här kommer vi inte att ta itu med Fourier-seriens expansion, utan kommer bara att använda en given summa av sines och kosinus som en excitation för en krets.

I de tidigare kapitlen i denna bok behandlade vi sinusoidal excitation. Om kretsen är linjär, superpositionsteori är giltig. För ett nätverk med nonsinusoidal periodisk excitation tillåter superposition oss beräkna strömmar och spänningar beroende på varje Fourier sinusoid en i taget. När alla beräknas sammanfattar vi slutligen de harmoniska komponenterna i svaret.

Det är lite komplicerat att bestämma de olika villkoren för de periodiska spänningarna och strömmarna och det kan faktiskt ge en överbelastning av information. I praktiken vill vi helt enkelt göra mätningar. Vi kan mäta de olika harmoniska termerna med a harmonisk analysator, spektrumanalysator, våganalysator eller Fourier-analysator. Alla dessa är komplicerat och ger förmodligen mer data än nödvändigt. Ibland räcker det att beskriva en periodisk signal endast med sina medelvärden. Men det finns flera typer av genomsnittliga mätningar.

GENOMSNITT VÄRDEN

Enkelt medelvärde or DC termen sågs i Fourier-representationen som A₀

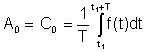
Detta medelvärde kan mätas med instrument som Deprez DC-instrument.

Effektivt värde or rms (root-medelkvadrat) har följande definition:

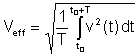
Detta är det viktigaste medelvärdet eftersom värmen som sprids i motstånd är proportionell mot det effektiva värdet. Många digitala och vissa analoga voltmetrar kan mäta det effektiva värdet på spänningar och strömmar.

Absolut medelvärde

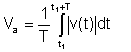
Detta genomsnitt är inte längre viktigt; tidigare instrument mätte denna form av genomsnitt.

Om vi ​​känner till Fourier-representationen av en spännings- eller strömvågform, kan vi också beräkna medelvärdena enligt följande:

Enkelt medelvärde or DC termen sågs i Fourier-representationen som A₀ = C₀

Effektivt värde or rms (root-medelkvadrat) är, efter integrering av Fourier-serien av spänningen:

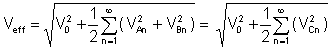
Smakämnen klirr-faktor är ett mycket viktigt förhållande mellan medelvärdena:

Det är förhållandet mellan det effektiva värdet för de högre harmoniska termerna till det effektiva värdet av den grundläggande harmoniken:

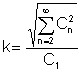
Det verkar finnas en motsägelse här - vi löser nätverk när det gäller harmoniska komponenter, men vi mäter genomsnittliga kvantiteter.

Låt oss illustrera metoden med enkla exempel:

Exempelvis 1

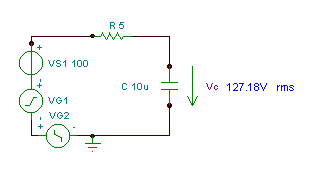
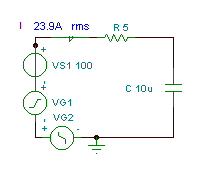
Hitta tidsfunktionen och det effektiva (rms) värdet för spänningen v_C(T)

Försök använda superpositionsteoremet för att lösa problemet.

Det första steget är att hitta överföringsfunktionen som en funktion av frekvensen. För att förenkla, använd substitutionen: s = j w

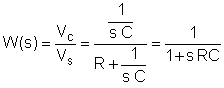
Byt ut komponentvärdena och s = jk w₀där k = 0; 1; 3 i detta exempel och w₀= 30 krad / s. I V, A, ohm, mF- och Mrad / s-enheter:

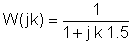
Det är bra att använda en tabell för att organisera stegen i den numeriska lösningen:

Vi kan sammanfatta stegen i superpositionslösningen i en annan tabell. Som vi redan har sett, för att hitta det komplexa toppvärdet för en komponent, bör vi multiplicera det komplexa toppvärdet för komponenten i excitationen med värdet på den komplexa överföringsfunktionen:

Och slutligen kan vi ge tidsfunktionen med kunskap om komplexa toppvärden för komponenterna:

v_C(t) = 100 + 110 cos (w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

Spänningens rms (effektiva) värde är:

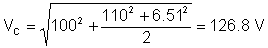
Som du kan se mäter TINA: s mätinstrument detta rms-värde.

Exempelvis 2

Hitta tidsfunktionen och det effektiva (rms) värdet för den aktuella i (t)

Försök lösa problemet med hjälp av superpositionsteoremet.

Byt nu ut de numeriska värdena och s = jk w_0,där k = 0; 1; 3 i detta exempel.

I V, A, ohm, mF- och Mrad / s-enheter:

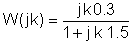
Det är bra att använda en tabell under den numeriska lösningen:

Vi kan sammanfatta stegen i superpositionen i en annan tabell. Som vi redan har sett, för att hitta en komponents toppvärde, bör vi multiplicera komplexa toppvärdet för den komponenten i excitationen med värdet på den komplexa överföringsfunktionen. Använd de komplexa toppvärdena för komponenterna i excitationen:

Och slutligen, genom att känna till komplexa toppvärden för komponenterna kan vi ange tidsfunktionen:

I (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [EN]

Than rms värdet på strömmen:

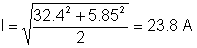
Du kan ofta göra en sanitetskontroll för en del av lösningen. Till exempel kan en kondensator ha en likspänning men inte en likström.

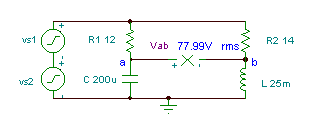
Exempelvis 3

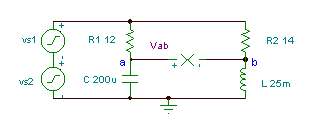
Skaffa tidsfunktionen för spänningen V_ab if R₁= 12 ohm, R₂ = 14 ohm, L = 25 mH och

Det första steget är att hitta överföringsfunktionen:

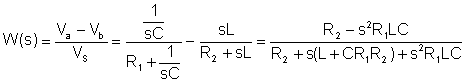
Att ersätta numeriska värden i V-, A-, ohm-, mH-, mF-, kHz-enheter:

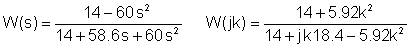
Sammanslagning av de två tabellerna:

k V Sk		V abk
0 50		50
1 80		79.3 och-j66.3
2 30 ej60		29.7 och-j44.7

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

och rms-värdet: