 Kliknite ili Dodirnite primjer krugova u nastavku da biste pozvali TINACloud i odaberite Interaktivni DC način za analizu na mreži.
Kliknite ili Dodirnite primjer krugova u nastavku da biste pozvali TINACloud i odaberite Interaktivni DC način za analizu na mreži. Nabavite jeftin pristup TINACloud uređivanju primjera ili stvaranju vlastitih krugova
U ovom i sljedećim poglavljima predstavit ćemo vrlo važnu temu: AC ili izmjenična struja. Naziv izmjenična struja nije vrlo precizan i normalno pokriva sklopove s sinusoidnim naponima i strujama; međutim, izmjenična struja također može značiti bilo koji proizvoljni valni oblik. Važnost izmjeničnog napona je da se takav napon koristi za glavni izvor električne energije u domovima i industriji diljem svijeta. To je također osnova mnogih elektroničkih, telekomunikacijskih i industrijskih aplikacija.
Kako bi se nosili s sinusoidnim valnim oblicima i s njima povezanim krugovima, koristit ćemo jednostavnu i elegantnu metodu nazvanu metoda fazora. Fazori se temelje na svojstvima kompleksnih brojeva, koji su idealni za predstavljanje sinusoidnih veličina. U ovom ćemo poglavlju sažeti glavne činjenice o složenim brojevima i njihovim operacijama. Također ćemo pokazati kako TINA-in Interpreter olakšava izračune sa složenim brojevima.
Kompleksni brojevi se sastoje od dva dijela, a stvarni dio (x), koji je pravi broj, i takozvani imaginarni dio (y), što je stvarni broj pomnožen s 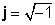
z = x + jy
gdje 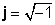
Primjeri složenih brojeva:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Složeni brojevi izvorno su uvedeni u sedamnaestom stoljeću kako bi predstavljali korijene polinoma koji se ne mogu predstaviti samo stvarnim brojevima. Na primjer, korijeni jednadžbe x2 + 2x + 2 = 0 može se opisati samo kao 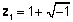
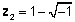
Geometrijski prikaz složenih brojeva
Pravokutni oblik
Budući da se složeni broj uvijek može odvojiti na njegove stvarne i složene dijelove, možemo složeni broj predstaviti kao točku na dvodimenzionalnoj ravnini. Stvarni dio složenog broja jest projekcija točke na stvarnu os, a imaginarni dio broja projekcija na imaginarnu os. Kad je složen broj predstavljen kao zbroj stvarnih i imaginarnih dijelova, kažemo da je u pravokutan or algebarski oblik.
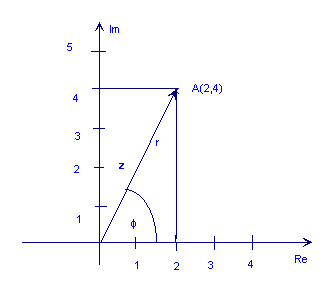
Sljedeća slika prikazuje složeni broj z = 2 + 4j
Polarni i eksponencijalni oblik
Kao što možete vidjeti na gornjoj slici, točka A mogla bi biti predstavljena i duljinom strelice, r (koja se također naziva apsolutna vrijednost, veličina ili amplituda) i njezin kut (ili faza), φ u odnosu na smjeru suprotnom od kazaljke na satu, do pozitivne vodoravne osi. Ovo je Polarni oblik složenog broja. Označava se kao r ∠ φ.
Sljedeći korak je vrlo važan. Složeni broj u polarnom obliku također se može upisati u eksponencijalan oblik:
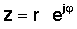
Ovaj jednostavan izraz karakterističan je po tome što ima imaginarni broj u eksponentu, umjesto uobičajenog stvarnog broja. Ovaj složen eksponencijal ponaša se vrlo različito od eksponencijalne funkcije stvarnim argumentom. Dok ex brzo raste u veličini za povećanje x> 0 i opadanje za x <0, funkcija 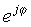
Eulerova formula pruža ujedinjujuću vezu između pravokutnih, polarnih i eksponencijalnih oblika kompleksnih brojeva:
z = x + jy = re jφ = r (cos φ + j bez φ )
gdje 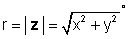
i φ = tan-1 (Y / x).
Za gore navedeni primjer, z = 2 + 4j:
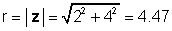
φ = tan-1 (4 / 2) = 63.4 °
stoga 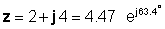
Ili obrnuto:
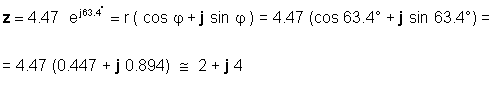
Morat ćete biti spretni u korištenju oba oblika, ovisno o aplikaciji. Na primjer, zbrajanje ili oduzimanje očito je lakše napraviti kada su brojevi u pravokutnom obliku, dok je množenje i dijeljenje lakše kada su brojevi u eksponencijalnom obliku.
Operacije sa složenim brojevima
Operacije koje se mogu obaviti složenim brojevima slične su operacijama za stvarne brojeve. Pravila i neke nove definicije sažeto su u nastavku.
Rad s j
Operacije s j jednostavno slijediti iz definicije imaginarne jedinice,


Da biste mogli raditi brzo i točno, trebali biste zapamtiti ova pravila:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 jednostavno slijedi iz definicije 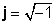
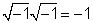
Za 1 /j, umnožavamo 1 /jby j / j = 1 i dobiti j/ (JJ) = j / (- 1) = -j.
Kompleksni konjugat
Kompleksni konjugat kompleksnog broja se lako izvodi i vrlo je važan. Da bismo dobili složeni konjugat kompleksnog broja u pravokutnom obliku, jednostavno promijenite znak imaginarnog dijela. Da biste to učinili za broj u eksponencijalnom obliku, promijenite znak kuta kompleksnog broja zadržavajući njegovu apsolutnu vrijednost istu.
Kompleksni konjugat kompleksnog broja z često označava z*.
S obzirom na složeni broj z= A + jb, njegov kompleksni konjugat je z*= a- jb.
If z je dano u eksponencijalnom obliku, 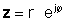
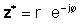
Koristeći gore navedene definicije, lako je vidjeti da kompleksni broj pomnožen složenim konjugatom daje kvadrat apsolutne vrijednosti kompleksnog broja:
ZZ* = r2 = a2 + b2
Također, dodavanjem ili oduzimanjem bilo kojeg kompleksnog broja i njegovog konjugata dobivamo sljedeće odnose:
z + z * = 2a
stoga
Re (z) = a = ( z + z * ) / 2
Slično:
z - z * =j2b
stoga
im (z) = b = ( z -z * ) / 2j
Dokaz:
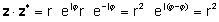
ili množenjem stvarnog i imaginarnog dijela i korištenja j2= -1
ZZ* = (A + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = A + jb + a - jb = 2a
z - z*= A + jb - a + jb =j2b
Brojčani primjeri:
U pravokutnom obliku:
z = + 3 j4
z* = 3- j4
ZZ * = 9 + = 16 25
U polarnom obliku
z = 5 ∠ 53.13 °
z * = 5 ∠ - 53.13 °
U eksponencijalnom obliku:
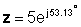
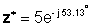
Zbrajanje i oduzimanje
Zbrajanje i oduzimanje složenih brojeva je jednostavno - stvarne i imaginarne dijelove trebamo samo dodavati. Na primjer, ako
z1 = 3 - 4j i z2 = 2 + 3j
tada
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Očito bismo trebali koristiti pravokutni oblik za ove operacije. Ako su brojevi dani u eksponencijalnom ili polarnom obliku, prvo ih moramo transformirati u pravokutni oblik koristeći Eulerovu formulu, kao što je dan ranije.
Množenje
Postoje dvije metode množenja kompleksnih brojeva -
Množenje složenih brojeva u pravokutnom obliku
Da biste izveli operaciju, jednostavno množite stvarne i imaginarne dijelove jednog broja zauzvrat stvarnim i imaginarnim dijelovima drugog broja i koristite identitet j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Kada su kompleksni brojevi dani numerički, nije potrebno koristiti gornju formulu. Na primjer, dopustite
z1 = 3 - 4j i z2 = 2 + 3j
S izravnim množenjem komponenti:
z1z2 = 3 - 4j(2 + 3j) = 6-8j +9j + 12 = 18 + j
ili pomoću formule: z1z2 = a1 a2- b1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Smatramo da je vjerojatnije da ćete pogriješiti ako koristite formulu nego ako izravno pomnožite komponente.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
uvezi matematiku kao m
import cmath kao c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
ispis(“z1*z2=”,z1*z2)
Množenje složenih brojeva u polarnom ili eksponencijalnom obliku
Da biste izvršili ovu operaciju, pomnožite apsolutne vrijednosti i dodajte kutove dva kompleksna broja. Neka:
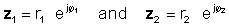
Zatim pomoću pravila množenja eksponencijalnih funkcija:
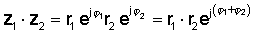
ili u polarnom obliku
z1 z2 = r1 r2 ∠ φ1 + φ2
Napomena: Ovo smo već koristili kada smo izračunali ZZ *iznad. Budući da kut konjugata ima suprotan znak izvornog kuta, složen broj pomnožen s vlastitim veznikom uvijek je stvaran broj; naime, kvadrat njegove apsolutne vrijednosti: ZZ * = r2
Na primjer, neka:
z1 = 5 ∠ 30 ° i z2 = 4 ∠ -60 °
tada
z1z2 = 20 ∠ -30 °
ili u eksponencijalnom obliku
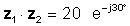
Množenje je očito jednostavnije kada su brojevi u polarnom ili eksponencijalnom obliku.
Međutim, ako su složeni brojevi navedeni u pravokutnom obliku, trebali biste razmotriti izvođenje množenja izravno kao što je prikazano gore, jer postoje dodatni koraci ako pretvorite brojeve u polarni oblik prije nego što ih množite. Drugi faktor koji treba razmotriti je da li želite da odgovori budu u pravokutnom obliku ili u polarnom / eksponencijalnom obliku. Na primjer, ako su dva broja u pravokutnom obliku, ali biste željeli da njihov proizvod bude u polarnom obliku, ima smisla odmah ih pretvoriti i potom množiti.
Podjela
Postoje dvije metode za dijeljenje kompleksnih brojeva -
Podjela složenih brojeva u pravokutnom obliku
Za izvođenje operacije pomnožite brojnik i nazivnik veznikom nazivnika. Nazivnik postaje stvarni broj, a dijeljenje se svodi na množenje dvaju složenih brojeva i dijeljenje na stvarni broj, kvadrat apsolutne vrijednosti nazivnika.
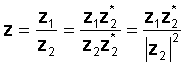
Na primjer neka:
z1 = 3 - 4j i z2 = 2 + 3j
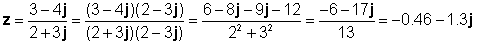
Provjerimo ovaj rezultat s TINA-inim Interpreterom:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
uvezi matematiku kao m
import cmath kao c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
ispis(“z1/z2=”,z1/z2)
Podjela kompleksnih brojeva u polarnom ili eksponencijalnom obliku
Za izvođenje operacije podijelite apsolutne vrijednosti (magnitude) i oduzmite kut imenitelja od kuta numeratora. Neka:
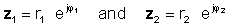
zatim pomoću pravila podjele eksponencijalnih funkcija
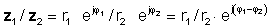
ili u polarnom obliku
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Na primjer, neka:
z 1 = 5 ∠ 30 ° i z 2 = 2 ∠ -60 °
tada
z 1 / z2 = 2.5 ∠ 90 °
ili u eksponencijalnim i pravokutnim oblicima
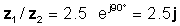
Provjerimo ovaj rezultat s TINA-inim Interpreterom:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
uvezi matematiku kao m
import cmath kao c
z1=5*(c.exp(kompleks(0,m.radijani(30))))
z2=2*(c.exp(kompleks(0,m.radijani(-60))))
ispis(“z1/z2=”,z1/z2)
Podjela je očito jednostavnija kada su brojevi u polarnom ili eksponencijalnom obliku.
Međutim, ako su složeni brojevi navedeni u pravokutnom obliku, trebali biste razmotriti izvođenje dijeljenja izravno složenom metodom konjugata kao što je prikazano gore, jer postoje dodatni koraci ako pretvorite brojeve u polarni oblik prije nego što ih podijelite. Drugi faktor koji treba razmotriti je da li želite da odgovori budu u pravokutnom obliku ili u polarnom / eksponencijalnom obliku. Na primjer, ako su dva broja u pravokutnom obliku, ali želite da njihov kvocijent bude u polarnom obliku, ima smisla odmah ih pretvoriti, a zatim ih podijeliti.
Sada ilustrirajmo korištenje složenih brojeva pomoću više numeričkih problema. Kao i obično, naša rješenja provjeravat ćemo pomoću TINA-inog tumača. Interpreter radi s radijanima, ali ima standardne funkcije za pretvorbu radijana u stupnjeve ili obratno.
Primjer 1 Pronađite polarni prikaz:
z = 12 - j 48
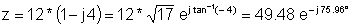
z: = 12-j * 48;
abs (z) = [49.4773]
luk (z) = [- 1.3258]
radtodeg (luk (z)) = [- 75.9638]
uvezi matematiku kao m
import cmath kao c
z=12-kompleks(48j)
ispis(“abs(z)=”,abs(z))
ispis(“luk(z)=”,c.faza(z))
print(“stupnjevi(luk(z))=”,m.stupnjevi(c.faza(z)))
Primjer 2 Pronađite pravokutni prikaz:
z = 25 e j 125 °
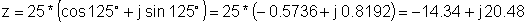
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
uvezi matematiku kao m
import cmath kao c
z=25*c.exp(kompleks(0,m.radijana(125)))
ispis(“z=”,z)
print(“real(z)=”,z.real)
print(“imag(z)=”,z.imag)
Primjer 3 Pronađite polarni prikaz sljedećih složenih brojeva:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Apsolutne vrijednosti sva četiri broja su iste jer je apsolutna vrijednost neovisna o znakovima. Samo su kutovi različiti.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
luk (z1) = [1.3258]
radtodeg (luk (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
luk (z2) = [- 1.3258]
radtodeg (luk (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
luk (z3) = [1.8158]
radtodeg (luk (z3)) = [104.0362]
z4: = - * j-12 48:
abs (z4) = [49.4773]
luk (z4) = [- 1.8158]
radtodeg (luk (z4)) = [- 104.0362]
uvezi matematiku kao m
import cmath kao c
z1=kompleks('12+48j')
ispis(“abs(z1)=”,abs(z1))
ispis(“luk(z1)=”,c.faza(z1))
print(“stupnjevi(luk(z1))=”,m.stupnjevi(c.faza(z1)))
z2=kompleks('12-48j')
ispis(“abs(z2)=”,abs(z2))
ispis(“luk(z2)=”,c.faza(z2))
print(“stupnjevi(luk(z2))=”,m.stupnjevi(c.faza(z2)))
z3=kompleks('-12+48j')
ispis(“abs(z3)=”,abs(z3))
ispis(“luk(z3)=”,c.faza(z3))
print(“stupnjevi(luk(z3))=”,m.stupnjevi(c.faza(z3)))
z4=kompleks('-12-48j')
ispis(“abs(z4)=”,abs(z4))
ispis(“luk(z4)=”,c.faza(z4))
print(“stupnjevi(luk(z4))=”,m.stupnjevi(c.faza(z4)))
TINA funkcija luka () određuje kut bilo kojeg složenog broja, automatski ga postavljajući pravilno u jedan od četiri kvadranta.
Budite oprezni, međutim, koristite tan-1 funkcija za pronalaženje kuta, jer je ograničen na povratne kutove samo u prvom i četvrtom kvadrantu (–90 °φ<90 °).
Od z1 nalazi se u prvom kvadrantu koordinatnog sustava, izračun je:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Od z4 nalazi se u trećem kvadrantu koordinatnog sustava, tan-1ne vraća kut ispravno. Izračun kuta je:
α 4 = 180 ° + 75.96 ° = 255.96 ° ili -360 ° + 255.96 ° = - 104.04 °, što je isto kao što je izračunao TINA.
z2 nalazi se u četvrtom kvadrantu koordinatnog sustava Izračun kuta je:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, međutim, nalazi se u 2nd kvadrantu koordinatnog sustava, tako tan-1 ne vraća kut ispravno. Izračun kuta je:
α 3 = 180 ° -75.96 ° = 104.04 °.
Primjer 4 Imamo dva kompleksna broja: z1= 4 - j 6 i z2 = 5 ej45 ° .
naći z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Prvo rješavamo problem pomoću TINA-inog tumača
{Rješenje TINA-ovog tumača} |
Primijetite kako TINA bez napora rukuje s dva složena broja u različitim oblicima.
Rješenje je složenije bez prevoditelja. Kako bismo mogli usporediti različite metode množenja i dijeljenja prvo ćemo odrediti polarni oblik z1 i pravokutni oblik z2 .
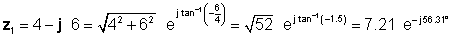
Zatim pronalazimo četiri rješenja koja najprije koriste najlakše oblike: pravokutna za zbrajanje i oduzimanje i eksponencijalna za množenje i dijeljenje:
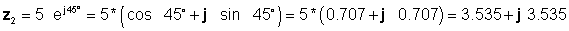
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
koji se slažu s rezultatima dobivenim s TINA tumačem.
Množenje provedeno u pravokutnom obliku:
z 5 =z1*z2 = (4-j6) * * 3.535 (1 +j) = 7.07 * (2-j3) + (+ 1j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Konačno, podjela provedena u pravokutnom obliku:
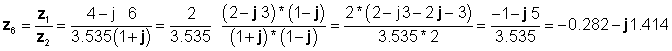
koji se slažu s prethodnim rezultatima.

