 Click or Tap the Example circuits below to invoke TINACloud and select the Interactive DC mode to Analyze them Online.
Click or Tap the Example circuits below to invoke TINACloud and select the Interactive DC mode to Analyze them Online. Get a low cost access to TINACloud to edit the examples or create your own circuits
Resistors dissipate energy in the form of heat, and the rate at which they dissipate energy is called power. The power dissipated by resistors is delivered by the voltage and/or current sources in the circuit.
The unit of power is the watt (one joule/second).
There are several ways of calculating the power of resistors.
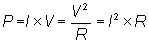
Example 1
Find the power of each circuit element if V=150 V and R = 1 kohm.
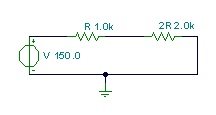
First, find the current of the network:
I = V /(R+2*R) =150/(1+2) = 150/3 = 50 mA
The power of the resistors is then:
P1 = I2 * R = 502 *10-6 *103 = 2.5 W;
P2 = I2 * 2*R = 502 *10-6 * 2*103 = 5 W;
The power delivered by the voltage source is:
PV = – I * V = – 5 * 10-2 *150 = -7.5 W.
Note that the current is opposite to the voltage in the source. By convention in this case, power is denoted as a negative quantity. If a circuit contains more than one source, some sources may actually dissipate energy if their current and voltage have the same direction.
The solution using TINA’s DC Analysis:
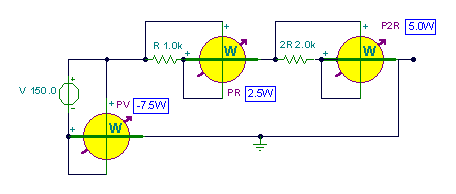
The simulation results agree with the calculated powers:
I:=V/(R+2*R);
P1:=I*I*R;
P2:=2*R*I*I;
P1=[2.5]
P2=[5]
PV:=-I*V;
PV=[-7.5]
I=V/(R+2*R)
P1=I*I*R
P2=2*R*I*I
print(“P1= %.3f”%P1)
print(“P2= %.3f”%P2)
PV=-I*V
print(“PV= %.3f”%PV)
We can calculate the power dissipated by each resistor if we know either the voltage or the current associated with each resistor. In a series circuit, it is simpler to find the common current, while in a parallel circuit it is easier to solve for the total current or the common voltage.
Example 2
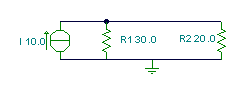
Find the power dissipated in each resistor if the source current is I = 10 A.
In this example, we have a parallel circuit. To find the power we must calculate the voltage of the parallel circuit:

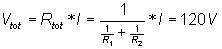
Find the power in each resistor:
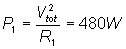
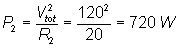

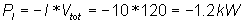
Solution using TINA’s DC Analysis
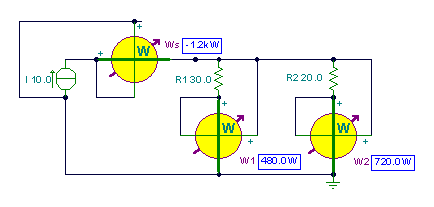
The simulation results agree with the calculated powers.
V:=I*Replus(R1,R2);
V=[120]
I1:=I*R2/(R1+R2);
I1=[4]
I2:=I*R1/(R1+R2);
I2=[6]
P1:=R1*sqr(I1);
P1=[480]
P2:=R2*sqr(I2);
P2=[720]
Ps:=-V*I;
Ps=[-1.2k]
Example 3
Find the power in the 5 ohm resistor.
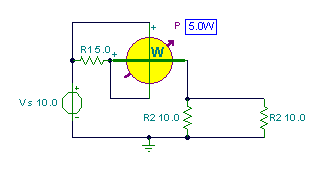
I:=Vs/(R1+Replus(R2,R2));
I=[1]
P5:=I*I*R1;
P5=[5]
Replus= lambda R1, R2 : R1*R2/(R1+R2)
I=Vs/(R1+Replus(R2,R2))
V1=Vs*R1/(R1+Replus(R2,R2))
P1=I*V1
print(“P1= %.3f”%P1)
Example 4
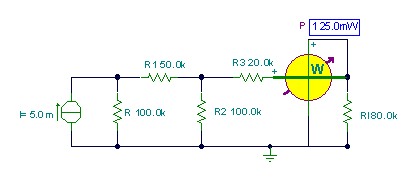
Find the power in the resistor RI.
Ir:=I*R/(R+R1+replus(R2,(R3+RI)))*R2/(R2+R3+RI);
Ir=[1.25m]
PRI:=sqr(Ir)*RI;
PRI=[125m]
Replus= lambda R1, R2 : R1*R2/(R1+R2)
Ii=I*R/(R+R1+Replus(R2,(R3+RI)))*R2/(R2+R3+RI)
Pi=Ii**2*RI
print(“Pi= %.3f”%Pi)