Click or Tap the Example circuits below to invoke TINACloud and select the Interactive DC mode to Analyze them Online.
Get a low cost access to TINACloud to edit the examples or create your own circuits

USING IMPEDANCE AND ADMITTANCE

SUPERPOSITION IN AC CIRCUITS

We have already shown how the elementary methods of DC circuit analysis can be extended and used in AC circuits to solve for the complex peak or effective values of voltage and current and for complex impedance or admittance. In this chapter, we’ll solve some examples of voltage and current division in AC circuits.

Example 1

Find the voltages v₁(t) and v₂(t), given that v_s(t)=110cos(2p50t).

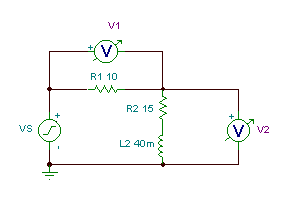
Let’s first obtain this result by hand calculation using the voltage division formula.

The problem can be considered as two complex impedances in series: the impedance of the resistor R1, Z₁=R₁ ohms (which is a real number), and the equivalent impedance of R₂ and L₂ in series, Z₂ = R₂ + j w L_2.

Substituting the equivalent impedances, the circuit can be redrawn in TINA as follows:

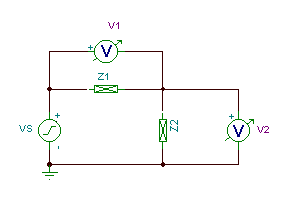
Note that we have used a new component, a complex impedance, now available in TINA v6. You can define the frequency dependence of Z by means of a table that you can reach by double clicking the impedance component. In the first row of the table you can define either the DC impedance or a frequency independent complex impedance (we have done the latter here, for the inductor and resistor in series, at the given frequency).

Using the formula for voltage division:

V₁ = V_s*Z₁ / (Z₁ + Z₂)

V₂ = V_s*Z₂ / (Z₁ + Z₂)

Numerically:

Z₁ = R₁ = 10 ohms

Z₂ = R₂ + j w L = 15 + j 2*p* 50*0.04 =15 + j 12.56 ohms

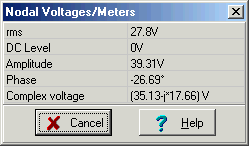
V₁= 110*10/ (25+j12.56) = 35.13-j17.65 V = 39.31 e ^{–j26.7 °} V

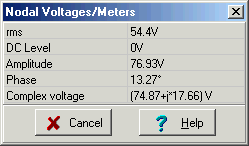
V₂= 110*(15+j12.56)/ (25+j12.56) = 74.86+j17.65 V = 76.92 e ^{j 13.3°} V

The time function of the voltages:

v₁(t) = 39.31 cos (wt – 26.7°) V

v₂(t) = 76.9 cos (wt + 13.3°) V

V1

V2

Next let’s check these results with TINA’s Interpreter:

Note that when using the Interpreter we did not have to declare the values of the passive components. This is because we are using the Interpreter in a work session with TINA in which the schematic is in the schematic editor. TINA’s Interpreter looks in this schematic for the definition of the passive component symbols entered into the Interpreter program.

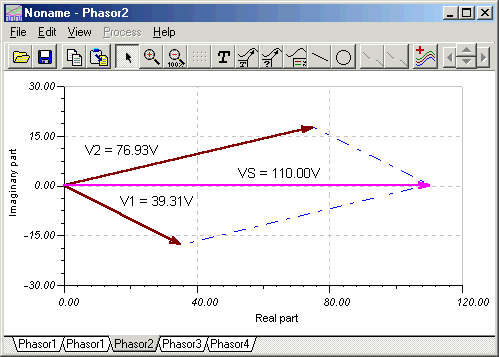
The diagram shows that V_s is the sum of the phasors V₁ and V₂, V_s = V₁ + V₂.

By moving the phasors we can also demonstrate that V₂ is the difference between V_s and V_1, V₂ = V_s – V_1.

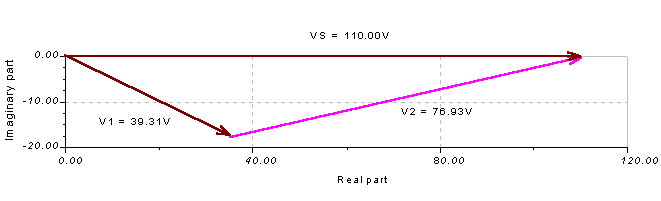
This figure also demonstrates the subtraction of vectors. The resultant vector should start from the tip of the second vector, V₁.

In a similar way we can demonstrate that V₁ = V_s – V_2. Again, the resultant vector should start from the tip of the second vector, V₁.

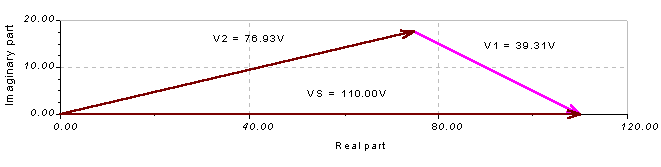
Of course, both phasor diagrams can be considered as a simple triangle rule diagram for V_s = V₁ + V₂ .

The phasor diagrams above also demonstrate Kirchhoff’s voltage law (KVL).

As we have learned in our study of DC circuits, the applied voltage of a series circuit equals the sum of the voltage drops across the series elements. The phasor diagrams demonstrate that KVL is also true for AC circuits, but only if we use complex phasors!

Example 2

In this circuit, R₁ represents the DC resistance of the coil L; together they model a real world inductor with its loss component. Find the voltage across the capacitor and the voltage across the real world coil.

L = 1.32 h, R₁ = 2 kohms, R₂ = 4 kohms, C = 0.1 mF, v_S(t) = 20 cos (wt) V, f = 300Hz.

V2

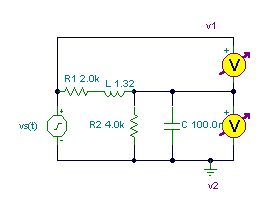
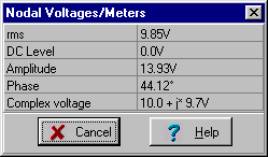
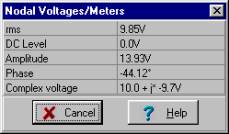
Solving by hand using voltage division:

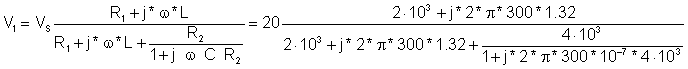
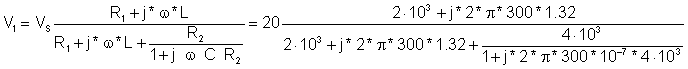
= 13.91 e ^{j 44.1°} V

and

v₁(t) = 13.9 cos (w×t + 44°) V

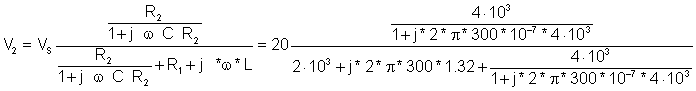
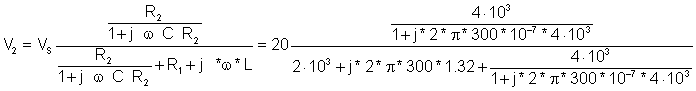
= 13.93 e ^{–j 44.1°} V

and

v₂(t) = 13.9 cos(w×t – 44.1°) V

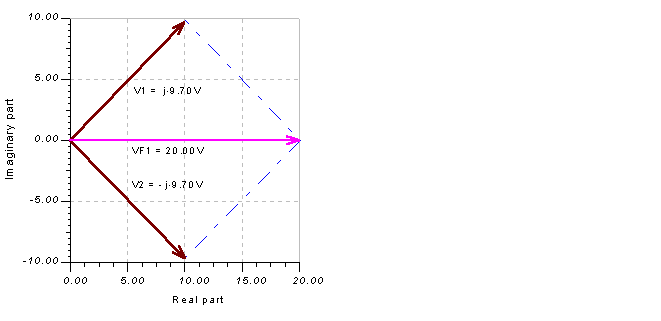
Notice that at this frequency, with these component values, the magnitudes of the two voltages are nearly the same, but the phases are of opposite sign.

Once again, let’s have TINA do the tedious work by solving for V1 and V2 with the Interpreter:

And finally, take a look at this result using TINA’s Phasor Diagram. Connecting a voltmeter to the voltage generator, invoking the Analysis/AC Analysis/Phasor Diagram command, setting the axes, and adding the labels will yield the following diagram (note that we have set View/Vector label style to Real+j*Imag for this diagram):

Example 3

IR

IL

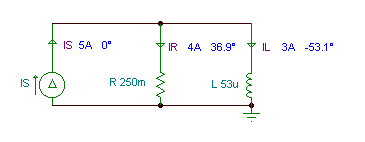
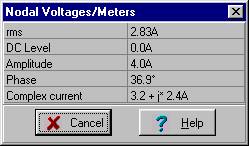
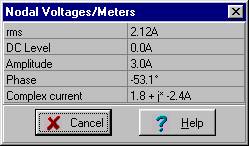
Using the formula for current division:

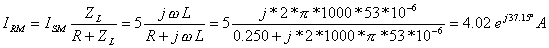
i_R(t) = 4 cos (w×t + 37.2°) A

Similarly:

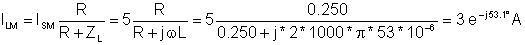
i_L(t) = 3 cos(w×t – 53.1°)

And using the Interpreter in TINA:

We can also demonstrate this solution with a phasor diagram:

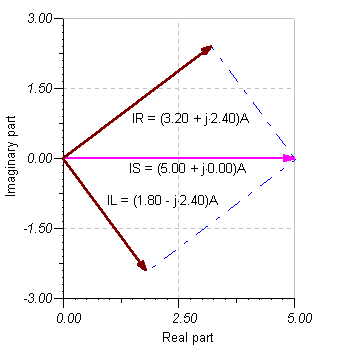
The phasor diagram shows that the generator current IS is the resultant vector of the complex currents IL and IR. It also demonstrates Kirchhoff’s current law (KCL), showing that the current IS entering the upper node of the circuit equals the sum of IL and IR, the complex currents leaving the node.

Example 4

Determine i₀(t), i₁(t) and i₂(t). The component values and the source voltage, frequency, and phase are given on the schematic below.

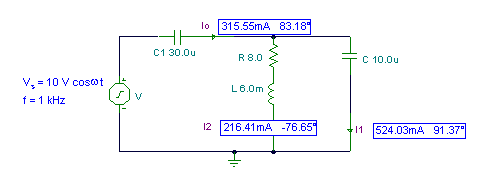
i₀

i₁

i₂

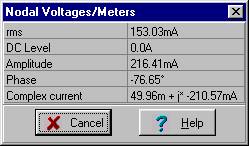
In our solution, we will use the principle of current division. First we find the expression for the total current i₀:

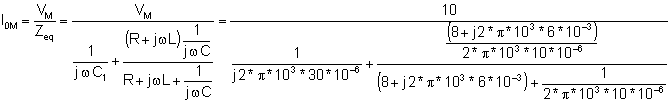
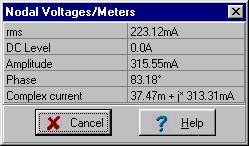
I_0M = 0.315 e ^{j 83.2°} A and i₀(t) = 0.315 cos (w×t + 83.2°) A

Then using current division, we find the current in the capacitor C:

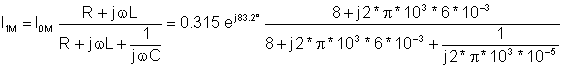
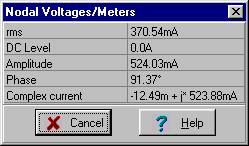
I_1M = 0.524 e ^{j 91.4°} A and i₁(t) = 0.524 cos(w×t + 91.4°) A

And the current in the inductor:

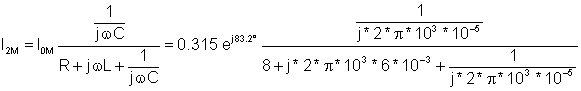
I_2M = 0.216 e^{–j 76.6°} A and i₂(t) = 0.216 cos(w×t – 76.6°) A

With anticipation, we seek confirmation of our hand calculations using TINA’s Interpreter.

Another way of solving this would be to first find the voltage across the parallel complex impedance of Z_LR and Z_C. Knowing this voltage, we could find the currents i₁ and i₂ by then dividing this voltage first by Z_LR and then by Z_C. We will show next the solution for voltage across the parallel complex impedance of Z_LR and Z_C. We will have to use the voltage division principal along the way:

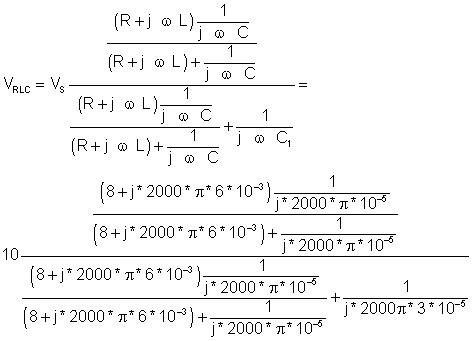
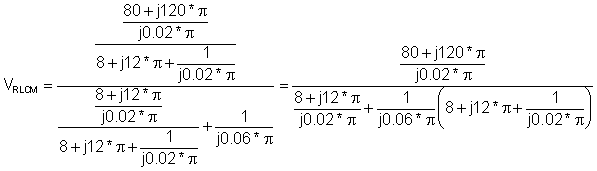
V_RLCM = 8.34 e ^{j 1.42°} V

and

I_C = I₁= V_RLCM*jwC = 0.524 e ^{j 91.42°} A

and hence

i_C (t) = 0.524 cos (w×t + 91.4°) A.

USING IMPEDANCE AND ADMITTANCE

SUPERPOSITION IN AC CIRCUITS