THÉVENIN A SEVER EQUIVALENT CIRCUITS

Klikněte nebo klepněte na níže uvedené okruhy příkladů, abyste vyvolali TINACloud a vyberte režim Interaktivní DC pro analýzu online.
Získejte levný přístup k TINACloudu pro editaci příkladů nebo vytvoření vlastních okruhů

KIRCHHOFFOVSKÉ ZÁKONY V AC CIRCUITS

Théveninova věta pro střídavé obvody se sinusovými zdroji je velmi podobná teorému, kterou jsme se naučili pro stejnosměrné obvody. Jediný rozdíl je v tom, že musíme zvážit impedance místo Odpor. Stručně řečeno, Théveninova věta pro střídavé obvody říká:

Jakýkoli dva terminální lineární obvody mohou být nahrazeny ekvivalentním obvodem sestávajícím ze zdroje napětí (VTh) a sériovou impedanci (ZTh).

Jinými slovy, Théveninova věta umožňuje nahradit komplikovaný obvod jednoduchým ekvivalentním obvodem obsahujícím pouze zdroj napětí a sériově zapojenou impedanci. Věta je velmi důležitá z teoretického i praktického hlediska.

Je důležité si uvědomit, že ekvivalentní obvod Thévenin poskytuje rovnocennost pouze na terminálech. Je zřejmé, že vnitřní struktura původního okruhu a ekvivalent Théveninů se mohou zcela lišit. A pro střídavé obvody, kde je impedance závislá na frekvenci, je ekvivalence platná na jedna frekvence.

Použití Théveninovy ​​věty je zvláště výhodné, když:

· chceme se soustředit na konkrétní část okruhu. Zbytek obvodu lze nahradit jednoduchým ekvivalentem Théveninu.

· musíme studovat obvod s různými hodnotami zatížení na terminálech. Použitím ekvivalentu Théveninu se můžeme vyhnout nutnosti analyzovat složitý původní obvod pokaždé.

Obvod ekvivalentu Théveninu můžeme vypočítat ve dvou krocích:

1. Vypočítaná ZTh. Nastavte všechny zdroje na nulu (nahraďte zdroje napětí zkratem a zdroje proudu otevřeným obvodem) a poté vyhledejte celkovou impedanci mezi oběma svorkami.

2. Vypočítaná VTh. Mezi svorkami zjistěte napětí naprázdno.

Nortonovu větu, která již byla uvedena pro stejnosměrné obvody, lze také použít v střídavých obvodech. Nortonova věta aplikovaná na střídavé obvody uvádí, že síť může být nahrazena a zdroj proudu paralelně s impedance.

Můžeme vypočítat ekvivalentní obvod Norton ve dvou krocích:

1. Vypočítaná ZTh. Nastavte všechny zdroje na nulu (nahraďte zdroje napětí zkratem a zdroje proudu otevřeným obvodem) a poté vyhledejte celkovou impedanci mezi oběma svorkami.

2. Vypočítaná ITh. Najděte zkratový proud mezi svorkami.

Nyní se podívejme na několik jednoduchých příkladů.

Příklad 1

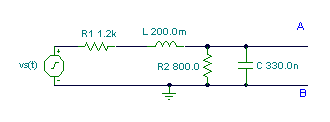
Najděte frekvenci Théveninu pro body A a B na frekvenci: f = 1 kHz, vS(t) = 10 cosw ×t V.


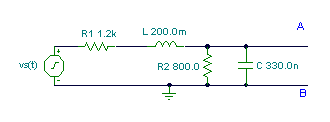
Klikněte / klikněte na výše uvedený obvod a analyzujte on-line nebo klikněte na tento odkaz Uložit pod Windows

Prvním krokem je nalezení napětí otevřeného obvodu mezi body A a B:

Napětí otevřeného obvodu pomocí dělení napětí:

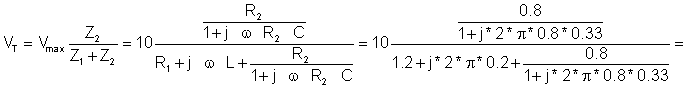
= -0.065 - j2.462 = 2.463 e-j91.5º V

Kontrola s TINA:


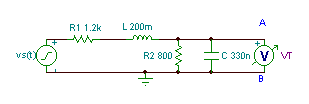
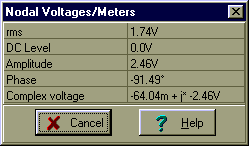
Druhým krokem je nahrazení zdroje napětí zkratem a nalezení impedance mezi body A a B:

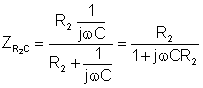
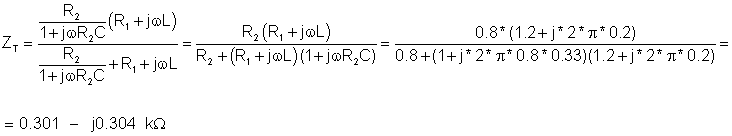
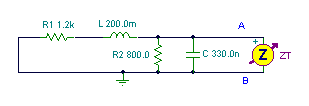
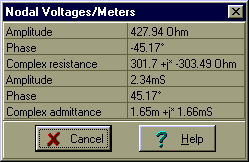
Samozřejmě můžeme zkontrolovat naši ZT řešení využívající impedanční měřič TINA (všimněte si, že jsme zdroj napětí nahradili zkratem):


Zde je ekvivalentní obvod Thévenin, platný pouze na frekvenci 1 kHz. Nejprve však musíme vyřešit kapacitu CT. Použití vztahu 1 /wCT = 304 ohm, najdeme CT = 0.524 uF

Nyní máme řešení: RT = 301 ohm a CT = 0.524 m F:

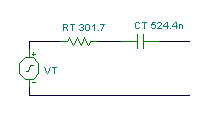
Dále můžeme použít tlumočník TINA ke kontrole našich výpočtů ekvivalentního obvodu Thévenin:

{Řešení od interpreta TINA}
VM: = 10;
f: = 1000;
om: = 2 * pi * f;
Z1: = R1 + j * om * L;
Z2: = R2 / (1 + j * om * C * R2);
VT: = VM * Z2 / (Z1 + Z2);
VT = [- 64.0391m-2.462 * j]
abs (VT) = [2.4629]
abs (VT) / sqrt (2) = [1.7415]
radtodeg (oblouk (VT)) = [- 91.49]
ZT: = Replus ((R1 + j * om * L), replus (R2, (1 / j / om / C)));
ZT = [301.7035-303.4914 * j]
Abs (ZT) = [427.9393]
radtodeg (oblouk (ZT)) = [- 45.1693]
Ct: = - 1 / im (ZT) / om;
Ct = [524.4134n]
#Řešení od Pythonu!
importovat matematiku jako m
importovat cmath jako c
#Zjednodušme tisk složitých
#numbers pro větší transparentnost:
cp= lambda Z : „{:.4f}“.format(Z)
#Definujte replus pomocí lambda:
Replus= lambda R1, R2: R1*R2/(R1+R2)
VM=10
f = 1000
om=2*c.pi*f
Z1=komplex(R1,om*L)
Z2=R2/komplex(1,om*C*R2)
VT=VM*Z2/(Z1+Z2)
print(“VT=”,cp(VT))
print(“abs(VT)= %.4f”%abs(VT))
print(“abs(VT)/sqrt(VT)= %.4f”%(abs(VT)/m.sqrt(2)))
print(“stupně(oblouk(VT))= %.4f”%m.stupně(c.fáze(VT)))
ZT=Replus(komplex(R1,om*L),Replus(R2,1/1j/om/C))
print(“ZT=”,cp(ZT))
print(“abs(ZT)= %.4f”%abs(ZT))
print(“stupně(oblouk(ZT))= %.4f”%m.stupně(c.fáze(ZT)))
Ct=-1/ZT.imag/om
print(“Ct=”,Ct)

Všimněte si, že ve výše uvedeném seznamu jsme použili funkci „replus“. Replus řeší paralelní ekvivalent dvou impedancí; tj. najde součin součtu dvou paralelních impedancí.

Příklad 2

Najděte ekvivalent obvodu Norton v příkladu 1.

f = 1 kHz, vS(t) = 10 cosw ×t V.


Klikněte / klikněte na výše uvedený obvod a analyzujte on-line nebo klikněte na tento odkaz Uložit pod Windows

Ekvivalentní impedance je stejná:

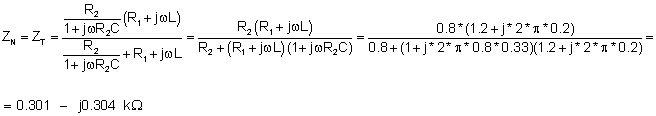
ZN= (0.301-j0.304) kW

Dále vyhledejte zkratový proud:

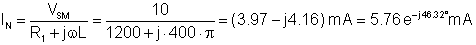
IN = (3.97-j4.16) mA

A můžeme porovnat naše ruční výpočty s výsledky TINA. Nejprve impedance otevřeného obvodu:


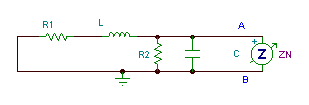
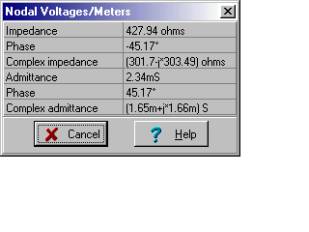
Pak zkratový proud:


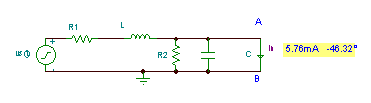
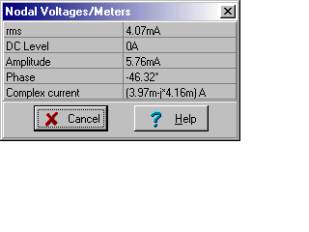
A konečně ekvivalent Norton:

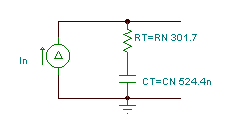
Dále můžeme použít překladač TINA k nalezení ekvivalentních komponent obvodu Norton:

{Řešení od interpreta TINA}
VM: = 10;
f: = 1000;
om: = 2 * pi * f;
Z1: = R1 + j * om * L;
Z2: = R2 / (1 + j * om * C * R2);
IN: = VM / Z1;
IN = [3.9746m-4.1622m * j]
abs (IN) = [5.7552m]
abs (IN) / sqrt (2) = [4.0695m]
radtodeg (oblouk (IN)) = [- 46.3207]
ZN: = Replus ((R1 + j * om * L), replus (R2, (1 / j / om / C)));
ZN = [301.7035-303.4914 * j]
Abs (ZN) = [427.9393]
radtodeg (oblouk (ZN)) = [- 45.1693]
CN: = - 1 / im (ZN) / om;
CN = [524.4134n]
#Řešení od Pythonu!
importovat matematiku jako m
importovat cmath jako c
#Zjednodušme tisk složitých
#numbers pro větší transparentnost:
cp= lambda Z : „{:.4f}“.format(Z)
#Definujte replus pomocí lambda:
Replus= lambda R1, R2: R1*R2/(R1+R2)
VM=10
f = 1000
om=2*c.pi*f
Z1=komplex(R1,om*L)
Z2=R2/komplex(1,om*C*R2)
IN=VM/Z1
print(“IN=”,cp(IN))
print(“abs(IN)= %.4f”%abs(IN))
print(“degrees(arc(IN))= %.4f”%m.degrees(c.phase(IN)))
print(“abs(IN)/sqrt(2)= %.4f”%(abs(IN)/m.sqrt(2)))
ZN=Replus(komplex(R1,om*L),Replus(R2,1/1j/om/C))
print(“ZN=”,cp(ZN))
print(“abs(ZN)= %.4f”%abs(ZN))
print(“stupně(oblouk(ZN))= %.4f”%m.stupně(c.fáze(ZN)))
CN=-1/ZN.imag/om
tisk (“CN=”,CN)

Příklad 3

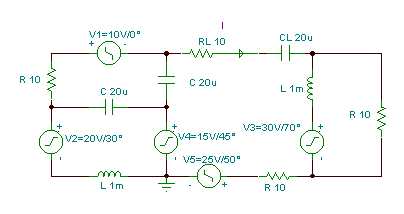
V tomto obvodu je zátěž sériově připojená RL a CL. Tyto komponenty zatížení nejsou součástí obvodu, jehož ekvivalent hledáme. Vyhledejte proud v zátěži pomocí ekvivalentu obvodu Norton.

v1(t) = 10 cos wt V; proti2(t) = 20 cos (wt + 30°) V; proti3(t) = 30 cos (wt + 70°) V;

v4(t) = 15 cos (wt + 45°) V; proti5(t) = 25 cos (wt + 50°) V; f = 1 kHz.


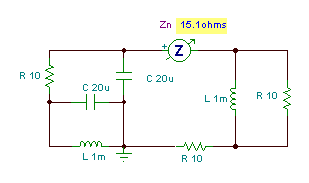
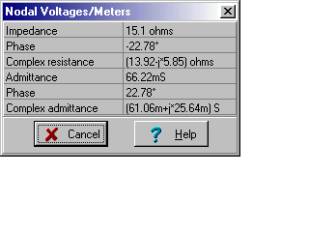
Klikněte / klikněte na výše uvedený obvod a analyzujte on-line nebo klikněte na tento odkaz Uložit pod Windows

Nejprve vyhledejte ekvivalentní impedanci otevřeného obvodu Zeq ručně (bez nákladu).

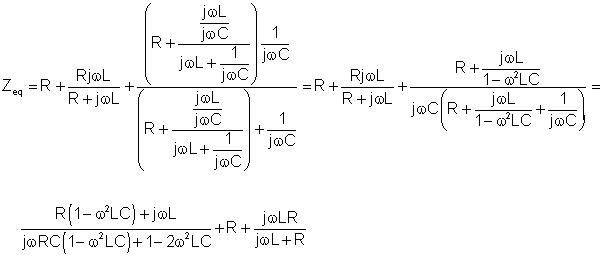
Numericky

ZN = Zeq = (13.93 - j5.85) ohm.

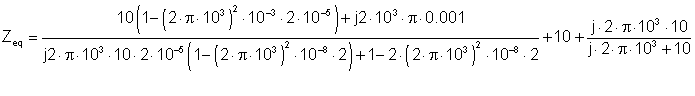
Níže vidíme řešení TINA. Před použitím měřiče jsme nahradili všechny zdroje napětí zkraty.


Nyní zkratový proud:

Výpočet zkratového proudu je poměrně komplikovaný. Tip: Toto by bylo dobré použít Superpozici. Přístup by spočíval v nalezení zátěžového proudu (v pravoúhlé formě) pro každý zdroj napětí odebraný po jednom. Pak sečtěte pět dílčích výsledků a získejte součet.

Použijeme pouze hodnotu poskytnutou společností TINA:

iN(t) = 2.77 cos (w ×t-118.27°) A


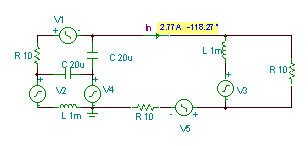
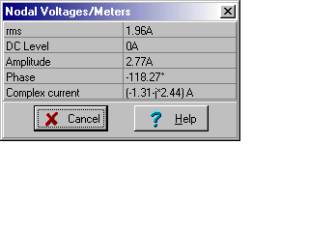
Když to dáme dohromady (nahrazení sítě ekvivalentem Norton, opětovné připojení komponent zatížení k výstupu a vložení ampéru do zátěže), máme řešení pro zátěžový proud, který jsme hledali:


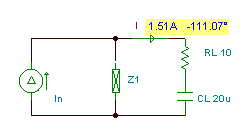
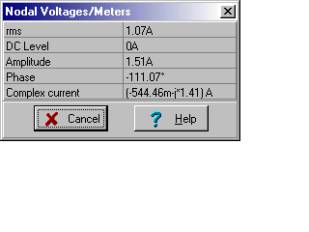
Pomocí ručního výpočtu jsme mohli zjistit zátěžový proud pomocí současného dělení:

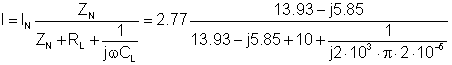
Konečně

I = (- 0.544 - j 1.41) A

a funkce času

i (t) = 1.51 cos (w ×t - 111.1°) A

{Řešení od interpreta TINA}
{Zkratovaný proud metodou mesh current}
om: = 2000 * pi;
V1: = 10;
V2:=20*exp(j*pi/6);
V3:=30*exp(j*pi/18*7);
V4:=15*exp(j*pi/4);
V5:=25*exp(j*pi/18*5);
SYS J1, J2, J3, J4
J1*(R-j*2/om/C)+V1+J2*j/om/C+J3*j/om/C=0
J1*j/om/C+J2*(j*om*L-j/om/C)+V4-V2=0
J1*j/om/C+J3*(R+j*om*L-j/om/C)-J4*j*om*L+V3+V5-V4=0
-J3*j*om*L+J4*(R+j*om*L)-V3=0
end;
J3=[-1.3109E0-2.4375E0*j]
{Impedance 'zabité' sítě}
ZLC:=j*om*L/(1-sqr(om)*L*C);
ZRL:=j*om*L*R/(R+j*om*L);
ZN:=(R+ZLC)/(1+j*om*C*(R+ZLC))+R+ZRL;
ZN=[1.3923E1-5.8456E0*j]
I:=J3*ZN/(ZN+RL-j/om/C);
I=[-5.4381E-1-1.4121E0*j]
#Řešení od Pythonu!
importovat matematiku jako m
importovat cmath jako c
#Zjednodušme tisk složitých
#numbers pro větší transparentnost:
cp= lambda Z : „{:.4f}“.format(Z)
om = 2000 x c.pi
V1 = 10
V2=20*c.exp(1j*c.pi/6)
V3=30*c.exp(1j*c.pi/18*7)
V4=15*c.exp(1j*c.pi/4)
V5=25*c.exp(1j*c.pi/18*5)
#Máme lineární systém rovnic
#které chceme vyřešit pro J1,J2,J3,J4:
#J1*(R-j*2/om/C)+V1+J2*j/om/C+J3*j/om/C=0
#J1*j/om/C+J2*(j*om*L-j/om/C)+V4-V2=0
#J1*j/om/C+J3*(R+j*om*L-j/om/C)-J4*j*om*L+V3+V5-V4=0
#-J3*j*om*L+J4*(R+j*om*L)-V3=0
import numpy jako n
#Napište matici koeficientů:
A=n.array([[komplex(R,-2/om/C),1j/om/C,1j/om/C,0],
[1j/om/C,1j*om*L-1j/om/C,0,0],
[1j/om/C,0,R+1j*om*L-1j/om/C,-1j*om*L],
[0,0,-1j*om*L,R+1j*om*L]])
b=n.array([-V1,V2-V4,V4-V3-V5,V3])
J1,J2,J3,J4=n.linalg.solve(A,b)
print(“J3=”,cp(J3))
#Impedance 'zabité' sítě
ZLC=1j*om*L/(1-om**2*L*C)
ZRL=1j*om*L*R/(R+1j*om*L)
ZN=(R+ZLC)/(1+1j*om*C*(R+ZLC))+R+ZRL
print(“ZN=”,cp(ZN))
I=J3*ZN/(ZN+RL-1j/om/C)
print(“I=”,cp(I))

KIRCHHOFFOVSKÉ ZÁKONY V AC CIRCUITS

    X
    Vítejte v DesignSoft
    Umožňuje chat, pokud potřebujete pomoc při hledání správného produktu nebo potřebujete podporu.
    wpchatıco
    en English
    en Englishde Germanfr Frenches Spanishpt Portugueseru Russianzh-CN Chinese (Simplified)zh-TW Chinese (Traditional)ja Japaneseko Koreanhu Hungarian