PARALLEL CONNECTED RESISTORS

Click or Tap the Example circuits below to invoke TINACloud and select the Interactive DC mode to Analyze them Online.
Get a low cost access to TINACloud to edit the examples or create your own circuits

SERIES CONNECTED RESISTORS

SERIES-PARALLEL CONNECTED RESISTORS

We say that two or more resistors are connected in parallel if the resistors are all connected to the same voltage. This causes the current to split into two or more paths (branches).

The voltage drop across each branch of a parallel circuit is equal to the voltage drop across all the other branches in parallel.

The sum of all the branch currents in a parallel circuit equals the total current.

From these two principles, it follows that the total conductance of a parallel circuit is the sum of all the individual resistor conductances. The conductance of a resistor is the reciprocal of its resistance.

Once we know the total conductance, the total resistance is easily found as the reciprocal of total conductance:

Example 1

Find the equivalent resistance!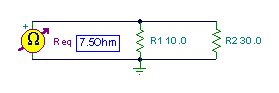

Click/tap the circuit above to analyze on-line or click this link to Save under Windows

We can use the two equations above to solve for the parallel equivalent of the two resistances by the formula:

You can also see the result calculated by TINA in the DC analysis mode, and as solved by TINA’s Interpreter.

{Solution by TINA’s Interpreter}
{Req=R1*R2/(R1+R2)}
Req:=Replus(R1,R2);
Req=[7.5]

#Solution by Python
Replus= lambda R1, R2 : R1*R2/(R1+R2)
Req=Replus(R1,R2)
print(“Req=”, Req)

Notice that the expression for Rtot (Req) in the Interpreter uses a special function for the calculation of the equivalent of two parallel connected resistances, Replus.

Example 2

Find the equivalent resistance of the three parallel connected resistors!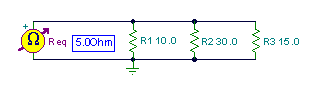

Click/tap the circuit above to analyze on-line or click this link to Save under Windows

{Solution by TINA’s Interpreter!}
{Req=1/(1/R1+1/R2+1/R3)
Req:=Replus(R1,Replus(R2,R3));
Req=[5]

#Solution by Python
Replus= lambda R1, R2 : R1*R2/(R1+R2)
Req=Replus(R1,Replus(R2,R3))
print(“Req=”, Req)

Here, in the Interpreter solution, you can see the application of Replus two times. The first time solves for Req of R2 and R3, the second time for the Req of R1 in parallel with the Req of R2 and R3.

Example 3

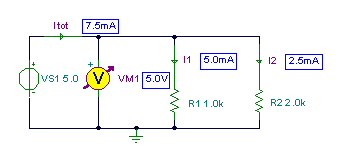
Click/tap the circuit above to analyze on-line or click this link to Save under Windows

Find the currents in the parallel connected resistors if the source voltage is 5 V!

{Solution by TINA’s Interpreter}
I1:=VS1/R1;
I1=[5m]
I2:=VS1/R2;
I2=[2.5m]
Itot:=I1+I2;
Itot=[7.5m]

#Solution by Python
I1=VS1/R1
print(“I1=”, I1)
I2=VS1/R2
print(“I2=”, I2)
Itot=I1+I2
print(“Itot=”, Itot)

In the Interpreter solution, we apply Ohms Law in a straightforward fashion to obtain the individual and total currents.

The following problem is a bit more practical

Example 4

An ammeter can safely measure currents up to 0.1 A without damage. When the ammeter is measuring 0.1A, the voltage across the ammeter is 10 m V. We wish to place a resistor (called a shunt) in parallel with the ammeter so that it can be used to safely measure a 2 A current. Calculate the value of this parallel connected resistor, R_P.

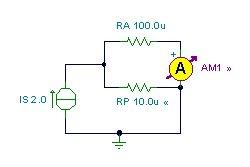
Click/tap the circuit above to analyze on-line or click this link to Save under Windows

Thinking through the problem, we realize that the total current will be 2A and that it must split, with 0.1A in our meter and with 1.9A in Rp. Knowing that the voltage across the ammeter and therefore also across the shunt is 10uV, we can use Ohm’s Law to find Rp = 10uV/1.9A, or 5.2632uOhms.

{Solution by TINA’s Interpreter !}
{First find the resistance of the ammeter}
Ia:=0.1;
Ua:=1e-5;
Ra:=Ua/Ia;
Ra=[100u]
Is:=2;
IP:=Is-Ia;
IP=[1.9]
Rp:=Ua/IP;
Rp=[5.2632u]

#Solution by Python
Ia=0.1
Ua=1E-5
Ra=Ua/Ia
print(“Ra=”, Ra)
Is=2
IP=Is-Ia
print(“IP=”, IP)
#let be RP = Ua/IP= Rc
Rc=Ua/IP
print(“Rc=”, Rc)

SERIES CONNECTED RESISTORS

SERIES-PARALLEL CONNECTED RESISTORS